

There are many ways of projecting a portion of a sphere, such as the surface of the Earth, onto a plane. In differential geometry, spherical geometry is described as the geometry of a surface with constant positive curvature.
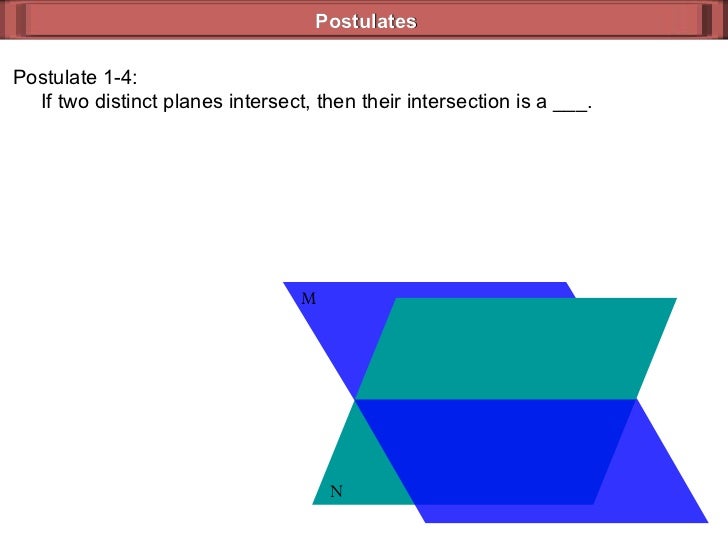
(Note, however, that intrinsically straight and shortest are not necessarily identical, as shown in the figure.) Three intersecting great circle arcs form a spherical triangle ( see figure) while a spherical triangle must be distorted to fit on another sphere with a different radius, the difference is only one of scale. Such curves are said to be “intrinsically” straight. This is a consequence of the properties of a sphere, in which the shortest distances on the surface are great circle routes. Great circles are the “straight lines” of spherical geometry. It has been demonstrated by mathematics that the surface of the land and water is in its entirety a sphere…and that any plane which passes through the centre makes at its surface, that is, at the surface of the Earth and of the sky, great circles. Get a Britannica Premium subscription and gain access to exclusive content. For example, the Greek astronomer Ptolemy wrote in Geography (c. Spherical geometryįrom early times, people noticed that the shortest distance between two points on Earth were great circle routes. It is this geometry that is called hyperbolic geometry. ( See geometry: Non-Euclidean geometries.) These attempts culminated when the Russian Nikolay Lobachevsky (1829) and the Hungarian János Bolyai (1831) independently published a description of a geometry that, except for the parallel postulate, satisfied all of Euclid’s postulates and common notions. If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, will meet on that side on which the angles are less than the two right angles.įor 2,000 years following Euclid, mathematicians attempted either to prove the postulate as a theorem (based on the other postulates) or to modify it in various ways. The second thread started with the fifth (“parallel”) postulate in Euclid’s Elements: These activities are aspects of spherical geometry. In addition to looking to the heavens, the ancients attempted to understand the shape of the Earth and to use this understanding to solve problems in navigation over long distances (and later for large-scale surveying). 300 bce) wrote about spherical geometry in his astronomical work Phaenomena. The first thread started with the search to understand the movement of stars and planets in the apparently hemispherical sky. The non-Euclidean geometries developed along two different historical threads. The sum of the interior angles of a triangle _ 180 degrees. Given a line and a point not on the line, there exist(s) _ through the given point and parallel to the given line.Įuclid’s fifth postulate is _.

SpaceNext50 Britannica presents SpaceNext50, From the race to the Moon to space stewardship, we explore a wide range of subjects that feed our curiosity about space!Ĭomparison of Euclidean, spherical, and hyperbolic geometries.Learn about the major environmental problems facing our planet and what can be done about them! Saving Earth Britannica Presents Earth’s To-Do List for the 21st Century.Britannica Beyond We’ve created a new place where questions are at the center of learning.

NON POSTULATE DEFINITION GEOMETRY HOW TO
COVID-19 Portal While this global health crisis continues to evolve, it can be useful to look to past pandemics to better understand how to respond today.Student Portal Britannica is the ultimate student resource for key school subjects like history, government, literature, and more.Britannica Explains In these videos, Britannica explains a variety of topics and answers frequently asked questions.Demystified Videos In Demystified, Britannica has all the answers to your burning questions.This Time in History In these videos, find out what happened this month (or any month!) in history.#WTFact Videos In #WTFact Britannica shares some of the most bizarre facts we can find.Britannica Classics Check out these retro videos from Encyclopedia Britannica’s archives.


 0 kommentar(er)
0 kommentar(er)
